The "mutilated chessboard" and end of class

Well, it's that time of year again; a bunch of final assignments due in the last week and exams on the horizon. I've enjoyed 236 quite a bit, and felt it introduced me to quite a few new and interesting concepts. I also appreciated Dan's enthusiasm throughout the course and willingness to help.

Anyways, after deliberating over what type of induction problem I found tricky throughout the course, I decided to write up the following one. Although once you understand the creative step in this problem it is quite simple, if you don't make the connection it is extremely difficult to formalize! These are the most interesting (and sometimes difficult) problems in my opinion; ones that require a non-obvious creative leap.

Prove by induction that a chessboard of any size (n x n), of at least size 2 x 2, with two black corners removed from it which are diagonal from each other, cannot be completed covered by a number of dominoes (each taking up two squares) equal to the total remaining squares on the board divided by 2.

Above, we see a diagram of the board for the typical 8x8 case and a representation of a domino below it.

Base case: n=2. Then, we would have one domino, and the board consists of two tiles diagonal from each other (i.e., no tiles which share an edge). Thus, it is clearly impossible to cover the board in this case.

Induction step: n>2. Assume that, for some j, the proposition to be proved holds. We want to show that it also holds for j+1. We notice that for a j x j board, there will be floor(j²/2) white tiles and ceil(j²/2)-2 black tiles. Thus, for a j+1 x j+1 board, there will be floor(j+1²/2) white tiles and ceil(j+1²/2)-2 black tiles. We can subtract the two values to see a pattern at each step. Specifically, the difference in either the black or the white tiles increases by 2 each time, but which one increases by 2 alternates at each step. Importantly, though, the white tiles are always increased by an even amount and the black by an odd amount. Thus, it follows that there are never the same amount of black tiles and white tiles added.

Since a domino must span 2 squares, it must be covering both a white tile and black tile. Since there are not an equal number of black tiles and white tiles, it is impossible to cover the added tiles with dominoes. And since it is also impossible to cover the tiles that were already there by the induction hypothesis, it is impossible to cover a j+1 x j+1 board with dominoes.

Conclude, by mathematical induction, that the proposition holds.

And that's that. Without noticing the trick with the tile colours, the proof is very tricky. In fact, the observation can be applied without using the inductive framework, but this was noticed only after attempting to use induction.

Anyways, have a great holiday everyone, and good luck on exams!

Converting state machines to regular expressions

Last week's tutorial/lecture finally made it clear how to translate a state machine to a regular expression (and vice versa) in practice. I liked being about to actually do it (rather than just understand it's possible in principle). For example:

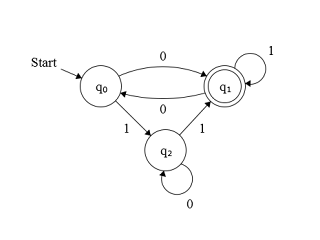
Starting with this machine, we can remove the non-starting, non-accepting state:

And at this point it becomes clear the strings which will drive the machine to the accepting state. Namely, the regular expression R for this machine is: R = (10*1+0)(1*0(10*1+0))*. As you can see, even for such a simple machine, the expression is pretty nasty (but the important thing is, it's possible)!

Regular expressions, and their equivalence to DFSAs

The recent lecture material on regular expressions has been pretty interesting, and I found it cool that every regular expression can, in principle, be represented by a DFSA (it makes sense, when you think about it).

The most recent lecture about "multiplying" DFSAs was also cool; by running many DFSAs in parallel you can find the intersection of strings accepted by each one (i.e., the set of strings accepted by all of them). This also makes intuitive sense, but makes it a lot easier to create complicated DSFAs by making each one act as a "filter" for a certain condition (as opposed to trying to make one from scratch that satisfies many conditions).

I've looked at the Assignment 3 questions, but due to a large Machine Learning project I haven't made much headway on it yet. I don't really understand loop invariants yet, so I'll need to read about them. The course notes have been a pretty useful resource the past few weeks, so I should be able to learn what I need from them.

I've noticed that I still haven't posted a specific "mathematical" problem on this blog yet, so I'll need to do that soon! I've found the material from the past 2 weeks or so to be the most interesting in the course so far, so it will probably be related to DSFAs and/or regular expressions.

Post-Test 2, and the beginning of finite state machines

Well, last week's test went decently. The one thing that kind of tripped me up, though, was the last question. After all we've done since the first test (e.g., proving that a function is non-decreasing, unwinding recurrence relations, etc.), I was definitely not expecting to rewrite a program function. It was either way too obvious and I overthought it (just square the first recursive call!), or I completely missed something subtle. We'll see.

Anyways, the topic of this week's lecture and tutorial seems pretty interesting. Back in high school, I had a final project for my geometry and discrete math class, and I decided to do it on cellular automata. I didn't go too deeply into the theory at that time (it was more a survey of the field), but even then I was impressed by some of the potential applications of it. I especially liked Conway's "Game of Life" (I even tried to write a simulator in Turing).

It looks as if the FSMs we will be working with (at least at first) take only binary strings as their inputs and accept or reject them. It will be interesting to see how the rules for designing and proving the correctness of FSMs like this can be applied to more complicated ones with more interesting inputs!

More recurrence relations, and bounds on complexity

In finishing up the second assignment, recurrence relations (particularly, the Fibonacci sequence) came up once again. Once I noticed the pattern, it was obvious to see that it was directly related to the Fibonacci sequence (one digit ahead of it), but I unwound it and recombined it to get some practice.

It's interesting how every recurrence relation which somehow involves the summing of the two previous numbers in the sequence has a closed form related to the golden ratio. In the Fibonacci case, the golden ratio satisfies the equations

so the powers of the golden ratio satisfy the Fibonacci recurrence. It's cool to see how it works!

In other news, I've been having some difficulty keeping up with all the new material that gets covered in tutorials. My tutorial section has been a little bit unhelpful in clarifying my difficulties. I plan to do whatever reading I have time to fit in before tutorials (although time is still at a premium).

Assignment 2 and allusions to Chomsky

Interestingly, in looking at the Assignment 2 questions and trying to learn about proving properties of binary strings, I stumbled upon the topic of "context-free grammars", which incidentally we are covering later in this course according to the schedule. I also learned they were originally described by Noam Chomsky, who I know about from his political writings. I very much admire Chomsky, and find the potential connection between formal languages in computer science and natural language very interesting!

Anyways, I'm admittedly having a bit of difficulty connecting the lecture material to the first question, and I hope that tonight's class will shed some light on that. The second question is more directly related to lecture material, and I can at least envision how to start. I'm happy the assignment is a bit shorter this time (or at least, appears to be; I might end up eating my words). Once I figure out how to solve questions like the first assignment problem, I'll probably write a post about it!

Post-Test, and starting "more practical" things

Well, we had our term test last week and I turned out to be pretty prepared for it, despite not feeling that way. The questions were all on structural and complete induction, so I didn't have trouble with the format, but two of them included recurrence relations which we didn't have a lot of practice with (other than talking about Fibonacci numbers relatively briefly in class). I was able to work them out and I think I did quite well, which is a good feeling!

The course seems to be changing flavour a bit now, and is starting to include reasoning about complexity of actual programs. I actually really like the purely theoretical proofs we've been doing -- it's fun to work them out, but it's also nice to do something which has a usefulness which is more immediate and apparent (even if it is, after all, still quite theoretical). It definitely has practical benefits, the first one coming to mind being comparing seemingly similar algorithms, which helps me stay motivated.

Anyways, this term has been a balancing act for me so far (a lot of commitments, school and otherwise), so it is good to get some positive feedback! I think my studying habits have been pretty reasonable for this course, but if I have trouble with the next assignment I might have to devote more time to it.